Contoh Soal Luas Permukaan Tabung / Contoh Soal Luas Permukaan Tabung - Contoh soal rumus luas permukaan tabung.

Agustus 04, 2021 Posting Komentar

Contoh Soal Luas Permukaan Tabung / Contoh Soal Luas Permukaan Tabung - Contoh soal rumus luas permukaan tabung.. Untuk membuat sebuah patung, pengrajin menggunakan sebuah batang pohon yang berbentuk seperti tabung dengan. Setelah mengetahui luas alas, luas tutup, dan luas selimut tabung, maka luas keseluruhan permukaan tabung bisa kita hitung dengan rumus: Cara menghitung luas permukaan balok. Dengan demikian, volume tabung sama dengan volume prisma, yaitu luas alas dikali tinggi. Sekarang kita lihat rumus luas permukaan tabung:

Luas permukaan tabung = 154 + 154 + 440. Materi ini telah dipelajari sejak duduk di bangku sekolah menengah pertama (smp) hingga sekolah menengah atas (sma). Untuk mengetahui rumus luas permukaan tabung beserta rumus luas alas, rumus volume, rumus luas selimut dan contoh soal, untuk lebih jelasnya simak pembahasan dibawah ini Luas permukaan tabung di peroleh dari = dua kali luas lingkaran + luas selimut yang berbentuk persegi panjang. Permukaan tabung tanpa tutup = π x r (r + 2t) l.

Rumus Volume & Luas Permukaan Tabung + Contoh Soal LENGKAP from www.nesabamedia.com

Jadi, luas permukaaan tabung adalah 748 cm2. Luas permukaan tabung = …? Contoh soal luas permukaan tabung. Contoh soal luas permukaan tabung. Untuk volum 100 liter, maka: Cara menghitung luas permukaan tabung. Luas alas = 154 cm 2. Oleh karena alas tabung berbentuk lingkaran, volume tabung dinyatakan sebagai berikut.

L = 2 (p x l + p x t + l x t) l = 2 (10 x 8 + 10 x 5 + 8 x 5) l = 2 (80 + 50 + 40) l = 2 x 170.

Hitunglah berapa luas permukaan tabung tersebut! Berapa volume dan luas permukaan tabung tersebut? Π = phi ( 22/7 atau 3,14 ). Untuk mengetahui rumus luas permukaan tabung beserta rumus luas alas, rumus volume, rumus luas selimut dan contoh soal, untuk lebih jelasnya simak pembahasan dibawah ini Jadi, luas permukaaan tabung adalah 748 cm2. Hal ini disebabkan karena banyaknya rumus yang harus dihafal. Luas permukaan tabung = luas alas + luas tutup + luas selimut. Pabrik kayu membentuk kayu hingga menjadi sebuah tabung atau silinder dengan luas penampang alas yaitu 340cm². Contoh soal rumus luas permukaan tabung. Berikut ini rumus rumus tabung/silinder (volume, luas permukaan & luas selimut), lengkap beserta contoh soal dan bagaimana cara menghitung yang benar !!! Rumus luas permukaan tabung = 2 x π x r x ( t + r ) dimana : Kita bisa latihan dengan contoh soal. Diketahui sebuah tabung berdiameter 20 cm dengan tinggi tabung adalah 24 cm.

Luas permukaan tabung menjadi salah satu materi di pelajaran matematika yang tidak jarang membuat kebingungan. Sekarang kita lihat rumus luas permukaan tabung: Luas selimut tabung = 792 cm 2; Π = phi ( 22/7 atau 3,14 ). Permukaan tabung tanpa tutup = 3,14 x 10 x (10 x 2 x 24)

Contoh soal luas permukaan tabung. Maka luas permukaan balok tersebut adalah…. Luas permukaan tabung = 2πr 2 + 2πr x t = 2πr (r + t) luas permukaan tabung tanpa tutup = πr (r + 2t) 3. Hitunglah luas permukaan dan volume dari tabung tersebut. Dengan demikian, volume tabung sama dengan volume prisma, yaitu luas alas dikali tinggi. Untuk π = 22/7 tentukanlah : Luas permukaan tabung = 2 x (π x r 2) + 2 x π x r x t = 2 x π x r x ( r + t ) untuk bisa lebih memahami hal ini, mari kita lihat salah satu contoh soal berikut ini: Π = phi ( 22/7 atau 3,14 ).

Untuk mengetahui rumus luas permukaan tabung beserta rumus luas alas, rumus volume, rumus luas selimut dan contoh soal, untuk lebih jelasnya simak pembahasan dibawah ini

Soal no.1 diketahui luas selimut tabung 1232 cm 2 dan luas alasnyanya 154 cm 2. L = 2 (p x l + p x t + l x t) l = 2 (10 x 8 + 10 x 5 + 8 x 5) l = 2 (80 + 50 + 40) l = 2 x 170. Hitunglah berapa luas permukaan tabung tersebut! L = 2 x π x r x (r + t) l = 2 x 22/7 x 7 x (7 + 10) l = 44 x 17 l = 748 cm² jadi, luas permukaan tabung tersebut adalah 748 cm². Luas permukaan tabung = 154 + 154 + 440. Contoh soal luas permukaan tabung. Luas permukaan tabung = …? Luas selimut = 440 cm 2. Jadi, luas permukaan tabung tanpa tutup tersebut adalah 34.464,94 cm 2. Maka luas permukaan balok tersebut adalah…. Π = phi ( 22/7 atau 3,14 ). Contoh soal bangun ruang sisi lengkung kelas 9. Kita bisa latihan dengan contoh soal.

Volume dari tabung tersebut volume π x r 2 x t 3 14 x 10 cm x 10 cm x 30 cm 942 cm 3 jadi volume dari tabung tersebut. Luas permukaan tabung = 2πr x (r+t) luas permukaan tabung = 2 × 22/7 × 0,7 × (0,7+2) luas permukaan tabung = 11,88 m² biaya yang dibutuhkan untuk mengecat tangki = 11,88 × 25.000 = 297.000 jadi, biaya yang dikeluarkan untuk mengecat tangki sebesar rp 297.000,00 pembahasan soal nomor 8 diketahui d = 3,5 m, r = 1,75 m dan v = 19.250 liter. Sebuah tabung memiliki panjang selimut 44 cm. Pada umumnya tabung yang dibelah menjadi dua dan diberikan papan pemisah akan menyebabkan bentuknya menjadi irisan. Luas permukaan tabung = 2 πr (t+r) = 44 x (10+7) = 44 x 17.

Bahan Ajar Tabung, Kerucut, dan Bola (Kelas IX) from image.slidesharecdn.com

Untuk membuat sebuah patung, pengrajin menggunakan sebuah batang pohon yang berbentuk seperti tabung dengan. Hal ini disebabkan karena banyaknya rumus yang harus dihafal. Contoh soal tabung dan jawabannya. L = 2 x π x r x (r + t) l = 2 x 22/7 x 7 x (7 + 10) l = 44 x 17 l = 748 cm² jadi, luas permukaan tabung tersebut adalah 748 cm². Cara menghitung luas permukaan tabung. Luas permukaan tabung = 2 x luas alas + luas selimut tabung. Luas permukaan tabung = 2πr x (r+t) luas permukaan tabung = 2 × 22/7 × 0,7 × (0,7+2) luas permukaan tabung = 11,88 m² biaya yang dibutuhkan untuk mengecat tangki = 11,88 × 25.000 = 297.000 jadi, biaya yang dikeluarkan untuk mengecat tangki sebesar rp 297.000,00 pembahasan soal nomor 8 diketahui d = 3,5 m, r = 1,75 m dan v = 19.250 liter. L = 2 x π x r x (r + t) l = 2 x 22/7 x 7 x (7 + 10) l = 44 x 17 l = 748 cm² jadi, luas permukaan tabung tersebut adalah 748 cm².

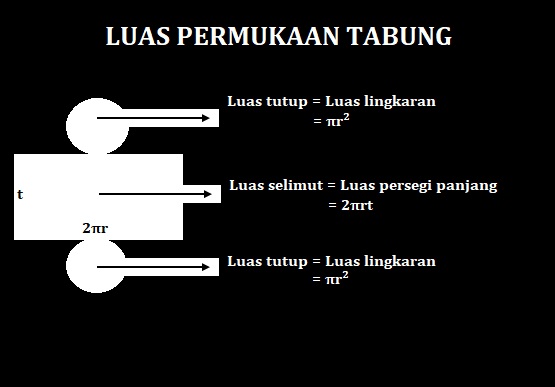
Rumus untuk mencari luas permukaan tabung adalah:

Jika luas selimut tabung 440 cm2, luas permukaan tabung tersebut adalah … penyelesaian : Luas permukaan tabung = …? Soal no.1 diketahui luas selimut tabung 1232 cm 2 dan luas alasnyanya 154 cm 2. V = π x r² x t v = 22/7 x 7² x 10 v = 22/7 x 49 x 10 v = 154 x 10 v = 1.540 cm³. L = 2 (p x l + p x t + l x t) l = 2 (10 x 8 + 10 x 5 + 8 x 5) l = 2 (80 + 50 + 40) l = 2 x 170. Luas permukaan tabung = luas alas + luas tutup + luas selimut. Luas alas = 154 cm 2. Hitunglah berapa luas permukaan tabung tersebut! Contoh soal menghitung luas permukaan tabung. Luas tutup = luas alas = 154 cm 2. Luas permukaan tabung = 2 πr (t+r) = 44 x (10+7) = 44 x 17. Luas permukaan tabung menjadi salah satu materi di pelajaran matematika yang tidak jarang membuat kebingungan. Untuk volum 100 liter, maka:

Sahil Erga